PBPK models
Most toxicity testing is done with laboratory animals. In order to estimate human health effects based on animal testing, two "extrapolations" are required. First, from observed high dose effects in the animal, an estimate of the low dose effects in the animal is made. This "high dose to low dose extrapolation" is a correct use of the word "extrapolation." Next, an estimate of the low dose human heath effects is made based on the estimate of the low does effects in the animal. This is often called the "animal to human extrapolation,." but this is not an extrapolation in the mathematical sense of the word. It is an assumption. Two different paths methods are used in this extrapolation process, one for carcinogens and one for non-carcinogens, but the net effect is the same.
A more scientific basis for these extrapolations is based on physiologically-based phamacokinetic (PBPK) modeling. Briefly, PBPK modeling tries to compare between species the dose of the chemical (or its activated metabolite) at the site of interest, a target organ or site within the organ. It is possible to reconcile these, because the absorption and distribution of a chemical in lab animals and humans is often known, and the kinetic parameters of metabolism and elimination are often known as well. For example, a mouse breaths (ventilates) at a rate of almost 10 times (on a body weight basis) a human. When examining the toxicity of a vapor in a mouse, the increased ventilation of the mouse might result in blood levels of the vapor much higher than a human would experience at the same vapor concentration. On a biochemical level, certain enzyme systems are different in the different species and even some organs are absent in one species. Many physiological parameters are quite well known. Some of the pharmacokinetic parameters are likewise known or determinative in the laboratory. Finally, many of the unknown parameters can be estimated based on known chemical properties, such as partitioning.
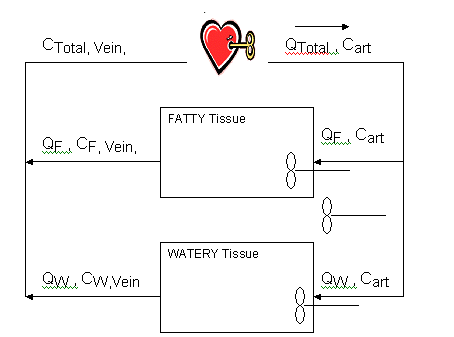
Lets suppose you gave a rat an an injection of styrene into the vena cave, the large vein that feeds into the heart, and we want to find the steady state concentration in the fatty tissues. Here's a simple model:
 |
Divide the body into two compartments, fatty tissue and water tissue (everything but fat). The cardiac output is Qtotal, the concentration of the chemical of interest in the arterial blood leaving the heart is Cart. The blood flow to the two compartments is different, QF for the fatty and QW for the watery. The little propellor symbol in each compartment means that it is a well-stirred compartment. Which means the concentration leaving the compartment is the same as the average concentration in the compartment, CF,Vein in the veins leaving the fatty tissue. Before the blood gets back to the heart, the concentrations from the two compartments, which are now different, will be combined with a weighted average into the CTotal, Vein. |
That leaves the questions unanswered, what is the concentration in the compartment? Well the concentration in a compartment is the amount (mass), we'll use "A" for amount, in the compartment divided by the volume. Here we use F subscript or the fatty tissue. CF = AF/VF (1). Where V is the volume of the fatty tissue.
So for each compartment, let's continuing use fatty for example, the change in the amount of styrene is the amount in the arterial blood that enters the compartment less the amount in the venous blood that leaves. So
change in amount = QF*(Cart - CF,Vein )
However since the concentration in the compartment is constantly changing, this should be expressed as a differential
dAF/dt = QF*(Cart - CF,Vein ) (2)
The concentration that leaves in the venous blood is related to the partition coefficient between blood and the tissue, PF, or
CVein =CF / PF (3), so putting (1) into (3) gives us: CVein = AF / (VF* PF)
and putting that into (2) yields
dA,F/dt = QF*(Cart - AF / (VF* PF) a first order linear differential equation. You write a similar equation for the watery compartment, just replace the "F" with "W." Note the parameters: QF,VF, PF are known from physiology, Cart is in this example given initially. So, you wind up with one differential equation for each compartment. If you had four compartments, fatty, muscle, richly profused tissue, and liver you would have four differential equations. These are related and must be solved simultaneously. There are several methods to solve these. One uses canned computer programs, PC non-lin was a favorite, there are many others. Another way is to use Excel. For that method you must use a finite dt, but its quite doable and the answers can be as close to exact as you want, just increase the number of cells.
An interesting variation on this, and its chief use for me, is in inhalation toxicokinetics. Hydrophobic gases are not well absorbed in the lungs, i.e., most of what is inhaled is exhaled. The amount absorbed is dependent on the amount already in the blood. The basic model is the same, but the arterial concentration is now related to the ventilation (breathing) rate, which is known from physiology, the concentration of the contaminant in the inhaled air, which is given, and blood / air partition coefficient, which is measurable in the laboratory.
Finally an elimination rate is set up in the liver or other tissue. Often the elimination rate is the unknown, and it that case the system can be solved for that rate, if the tissue concentrations are known.
Next is a diagram of a four compartment model and a table of parameters. Note all the parameters, except possibly the metabolism rates, are readily available from the literature, or easily measured in the laboratory.